Japanische Wissenschaftler entdecken eine neue Methode, um „Schwarzen Löchern zuzuhören“

Stellen Sie sich vor, ein Schwarzes Loch kollidiert mit einem anderen, und obwohl wir nichts „hören“, vibriert die gesamte Raumzeit. Wir bezeichnen diese Wellen als quasi-normale Moden, die im Wesentlichen Echos der Störung sind, wie unsichtbare Glocken, die kurz läuten, bevor sie sich in Nichts auflösen.

Diese „Echos“ und ihre Frequenzen enthalten wichtige Informationen über die Masse, Größe und sogar Form des Schwarzen Lochs, das nach der Kollision zurückbleibt. Die Messung dieser Parameter ist im Wesentlichen das Lauschen auf den Gesang der Tiefe, aber ihre genaue Berechnung war bisher eine technische Herausforderung.

Am schwierigsten sind die stark gedämpften Moden, da sie schnell abklingen. Detektoren können zwar die stärksten Moden erkennen, aber um die schwächsten zu verstehen, sind Formeln erforderlich, die heikle mathematische Grenzen überschreiten. Hier kommt ein leistungsstarkes, aber wenig genutztes Werkzeug der Physik zum Einsatz: die exakte WKB-Methode.

Eine Gruppe japanischer Forscher unter der Leitung von Taiga Miyachi beschloss, diese Methode auf die Untersuchung von Schwarzen Löchern anzuwenden, und was sie entdeckten, war überraschend: verborgene Spiralmuster, unsichtbare Schnitte in der Mathematik des Horizonts und eine neue Methode, um die Wellen zu verfolgen, die aus der Dunkelheit ins Unendliche dringen.

Mit dieser Technik konnten sie die Schwingungen der Raumzeit vom Horizont des Schwarzen Lochs bis in weit entfernte Regionen genau nachverfolgen und Strukturen auflösen, die zuvor nicht erreichbar waren. Darüber hinaus gelang ihnen dies ohne Rückgriff auf numerische Simulationen, sondern nur mit Papier und Bleistift und einer Menge komplexer Mathematik.

Was ist die WKB-Methode (und warum ist sie so besonders)?

Es handelt sich um eine Technik, die ihren Ursprung in der Quantenmechanik hat und zur Lösung komplexer Gleichungen dient, ohne deren genaue Lösung zu kennen. Ihre „exakte” Version ermöglicht es außerdem, diese Lösungen auf die komplexe Ebene auszuweiten, wodurch Verhaltensweisen sichtbar werden, die mit herkömmlichen Methoden unbemerkt bleiben.

Im Gegensatz zu anderen Ansätzen erfordert die exakte WKB-Methode weder das Schließen beliebiger Konturen noch die Annahme extremer Grenzwerte und kann direkt auf der reellen Zahlengeraden angewendet werden. Anschließend werden die globalen Lösungen der Differentialgleichungen analysiert, was einen grundlegenden Schritt bei der Beschreibung von Raum-Zeit-Schwingungen darstellt.

Eines der zentralen Konzepte sind die Stokes-Kurven, die unsichtbaren Grenzen, an denen sich die Beschaffenheit einer Welle abrupt ändert, und es stellt sich heraus, dass diese Kurven keine einfachen Linien sind, sondern unendliche logarithmische Spiralen bilden können, die aus dem Horizont des Schwarzen Lochs hervorgehen.

Diese Spiralen wurden in vielen früheren Studien übersehen. Sie waren jedoch entscheidend für das Verständnis, wie Lösungen in der Nähe des Schwarzen Lochs mit denen in Verbindung stehen, die den fernen Weltraum beschreiben, da sie in gewisser Weise die Wege sind, auf denen Gravitationsechos wandern.

Eine mathematische Symphonie in einer Spirale

Durch die Anwendung der exakten WKB-Methode auf ein Schwarzschild-Schwarzes Loch entdeckten die Forscher eine reichhaltige und präzise Struktur in den Quasinormalmoden – tatsächlich konnten die schwächsten und gedämpften Moden, die zuvor schwer vorherzusagen waren, elegant berechnet werden.

Um ihren Ansatz zu validieren, testeten sie die Methode zunächst an einfachen Modellen wie dem harmonischen Oszillator und dem Morse-Potential , Systemen, die zwar klassisch sind, aber strukturelle Ähnlichkeiten mit den Gleichungen der Raumzeit um ein Schwarzes Loch aufweisen.

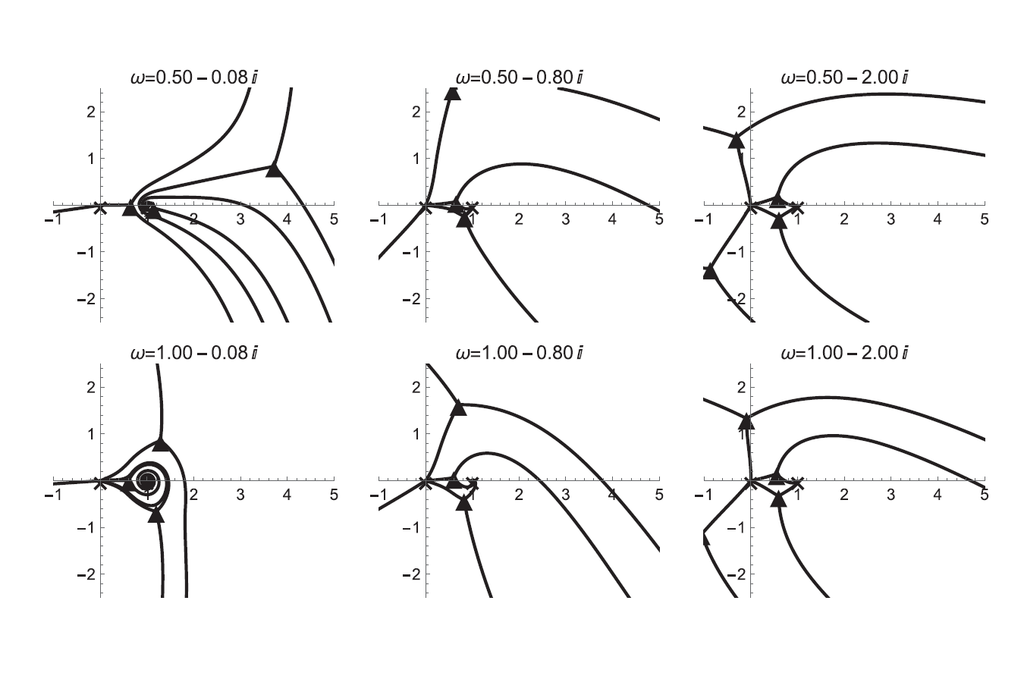
Die wichtigste Entdeckung war, dass das Verhalten von Stokes-Kurven um singuläre Punkte in der Raumzeit einen direkten Einfluss auf die Echo-Frequenzen hat. Durch die Berücksichtigung dieser mathematischen Spiralen konnte das Team die erforderlichen Randbedingungen genau abstimmen.

Auf diese Weise lösten sie nicht nur exakte Modelle, sondern öffneten auch die Tür zur Berechnung der tatsächlichen Frequenzen, die ein Schwarzes Loch nach einer Verschmelzung aussendet. So etwas wie eine mathematische Symphonie, die wir bisher zwar gehört, deren Partitur wir aber nicht kannten.

Das Universum zeichnet mit einem Echo

Dieser Fortschritt ist nicht nur theoretischer Natur, denn Gravitationswellen, die von Observatorien wie LIGO oder KAGRA erfasst werden, könnten mit größerer Präzision analysiert werden, wenn wir ihre subtileren Komponenten besser verstehen würden, und genau das ermöglicht diese neue mathematische Formulierung.

Jeder quasiklassische Modus ist wie eine Note im Lied des Universums. Wenn man weiß, wie man sie interpretiert, wie es ein kosmisches Orchester tun würde, könnte man erkennen, ob es sich bei einem beobachteten Objekt um ein klassisches Schwarzes Loch oder um etwas Exotischeres handelt , wie beispielsweise einen bosonischen Stern oder einen noch unbekannten Quantenrest.

Das Team plant nun, seine Analyse auf rotierende oder Kerr-Schwarze Löcher auszuweiten, bei denen die Geometrie noch komplexer ist, und zu untersuchen, wie diese Methode auf Theorien jenseits der allgemeinen Relativitätstheorie angewendet werden kann, einschließlich möglicher Quanteneffekte in der Gravitation.

Diese Arbeit löst nicht nur ein altes Problem, sondern eröffnet auch einen neuen Weg, um aufmerksam und genau auf die tiefsten Geheimnisse des Universums zu hören, denn manchmal verbirgt sich hinter scheinbarer absoluter Stille das aufschlussreichste Echo.

Quellenhinweis:

Path to an exact WKB analysis of black hole quasinormal modes. Taiga Miyachi, Ryo Namba, Hidetoshi Omiya, Naritaka Oshita. Phys. Rev. D 111, 124045. Published 24 June, 2025.